Dimensionnement de Structures : Sollicitations simples
Résumé de section
-
La contrainte est une action interne à la matière répartie sur la section. Elles équilibrent les actions extérieures. La résultante de ces actions réparties sont par définition égale au torseur de cohésion. Si on prend une facette dont la normale est celle de la section, les contraintes \( \sigma \) sont normales à la section. Par définition, la résultante de ces contraintes normales est l'effort normal du torseur de cohésion
\( N = \int_S \sigma dS \)
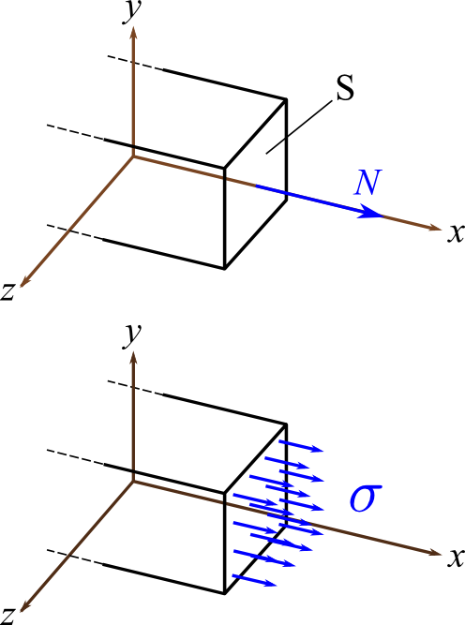
Si la contrainte est constante dans toute la section, on a :
\( N=\sigma S \) ou encore \( \sigma = \frac{N}{S} \)
Le tenseur de contrainte s'écrit pour tout point de la section:
\( \left [ \begin{matrix} \sigma & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0\end{matrix} \right ]_{\vec{x}\vec{y}\vec{z}} \)
-
Idem, pour la contrainte de cisaillement (ou tangentielle) dans la section. On obtient le même genre de relation : \( \tau= \frac{T_y}{S} \)
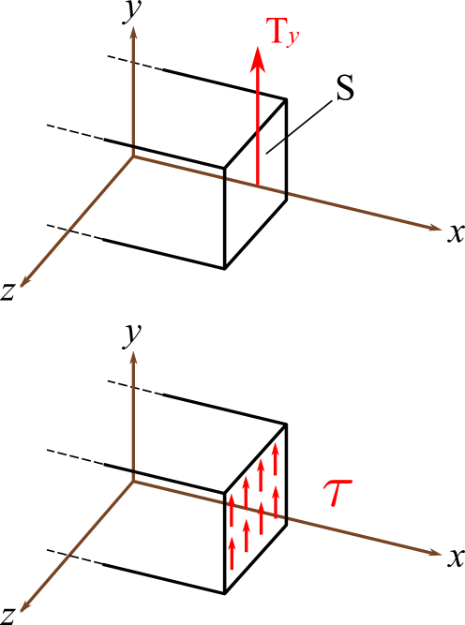
Pour la plupart des structures, les contraintes de cisaillement liées à l'effort tranchant sont bien souvent négligées.
Le tenseur des contraintes s'écrit:
\( \left [ \begin{matrix} 0 & \tau & 0 \\ \tau & 0 & 0 \\ 0 & 0 & 0 \end{matrix} \right ]_{\vec{x}\vec{y}\vec{z}} \)
-
Pour la flexion, le moment résultant induit par les contraintes : \( M_f = \int \sigma y dS \)
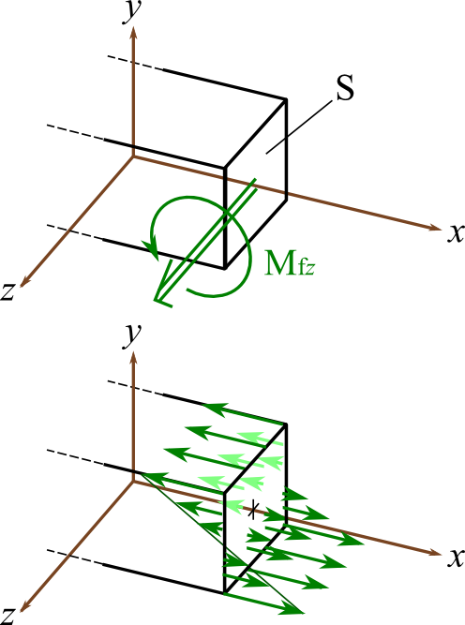
Après quelques calculs, on peut montrer que
\( \sigma = - \frac{M_{fz}}{I_{Gz}} y \)
On remarque que les contraintes ne sont plus homogènes dans la section et qu'elles dépendent de leur position par rapport au centre de la section (ligne neutre).
Le tenseur des contraintes s'écrit:\( \left [ \begin{matrix} \sigma(y)$& 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{matrix} \right ]_{\vec{x}\vec{y}\vec{z}} \)
Exemple
Une poutre rectangulaire de 100mm de haut et 50 mm de large et 4mm d'épaisseur subit un moment fléchissant de 500000N.mm. Déterminer la contrainte en y=0 et y =50mm.
Calcul de I = \( \frac{100^3 50}{12}-\frac{92^3 42}{12}=1441258mm^4 \)
en y= 0, la contrainte est nulle
en y =50mm, la contrainte vaut \( -\frac{5000000}{1441258}50=-173MPa \)
-
On traite principalement la torsion de barreau cylindrique en détail. Les autres types de sections seront brièvement détaillées.
Barreau cylindrique
La contrainte de cisaillement s'écrit:
\( \tau = \frac{M_t}{J} r \)
avec \( J=\pi\frac{D^4}{32} \)
et le tenseur de contraintes dans un repère cylindrique:
\( \left [ \begin{tabular}{ccc} 0 & $\tau$ & 0 \\ $\tau$ & $0$ & $0$ \\ $0$ & $0$ & $0$\end{tabular} \right ]_{\vec{x}\vec{y}\vec{z}} \cdot \)
Autres sections
Dans le cas des parois minces fermées d'épaisseur constante (e), on a la relation suivante:\( \tau e = \frac{M_t}{A} \)où A est l'aire de la surface de la ligne pointillée.
-
En général, ces sollicitations sont composées entre elles:
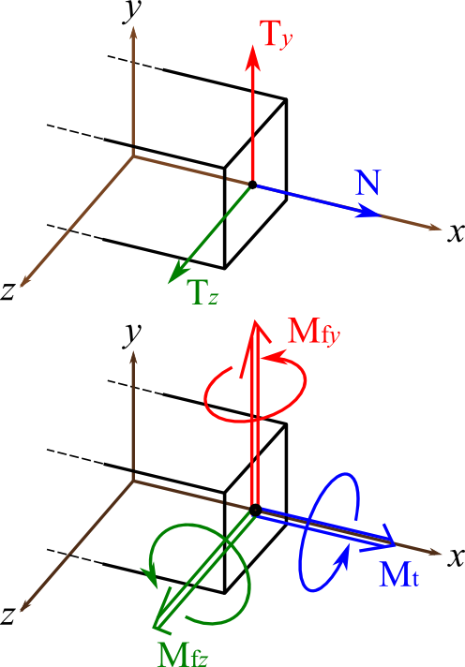
Dans ces conditions, les contraintes en un point s'additionnent.
Traction + Flexion sur z
Si on a le torseur de cohésion qui s'écrit:\( _G \left \{ \begin{tabular}{cc} N & $0$ \\ $0$ & $0$ \\ $0$ & $M_{f3}$\end{tabular} \right \}_{\vec{x}\vec{y}\vec{z}} \)L'effort normal crée des contraintes normales et uniformes dans la section:\( \left [ \begin{tabular}{ccc} $\sigma=\frac{N}{S}$ & 0 & 0 \\ 0 & $0$ & $0$ \\ $0$ & $0$ & $0$\end{tabular} \right ]_{\vec{x}\vec{y}\vec{z}} \cdot \)et la flexion autour de z (3) crée une contrainte qui varie dans la section:\( \left [ \begin{tabular}{ccc} $\sigma(y)=-\frac{M_{f3}}{I_{G3}} y$ & 0 & 0 \\ 0 & $0$ & $0$ \\ $0$ & $0$ & $0$\end{tabular} \right ]_{\vec{x}\vec{y}\vec{z}} \cdot \)au bout du compte, on a en tout point de la section:\( \left [ \begin{tabular}{ccc} $\frac{N}{S}-\frac{M_{f3}}{I_{G3}} y$ & 0 & 0 \\ 0 & $0$ & $0$ \\ $0$ & $0$ & $0$\end{tabular} \right ]_{\vec{x}\vec{y}\vec{z}} \cdot \)Torsion - Flexion d'un barreau cylindrique
Le torseur de cohésion s'écrit:\( _G \left \{ \begin{tabular}{cc} 0 & $M_t$ \\ $0$ & $0$ \\ $0$ & $M_{f3}$\end{tabular} \right \}_{\vec{x}\vec{y}\vec{z}} \)La flexion crée un état de contrainte:\( \left [ \begin{tabular}{ccc} $\sigma(y)=-\frac{M_{f3}}{I_{G3}} y$ & 0 & 0 \\ 0 & $0$ & $0$ \\ $0$ & $0$ & $0$\end{tabular} \right ]_{\vec{x}\vec{y}\vec{z}} \cdot \)et la torsion:\( \left [ \begin{tabular}{ccc} 0 & $\frac{M_t}{J}r$ & 0 \\ $\frac{M_t}{J}r$ & $0$ & $0$ \\ $0$ & $0$ & $0$\end{tabular} \right ]_{\vec{x}\vec{y}\vec{z}} \cdot \)Le tenseur des contraintes en un point s'écrit alors:\( \left [ \begin{tabular}{ccc} $-\frac{M_{f3}}{I_{G3}} y$ & $\frac{M_t}{J}r$ & 0 \\ $\frac{M_t}{J}r$ & $0$ & $0$ \\ $0$ & $0$ & $0$\end{tabular} \right ]_{\vec{x}\vec{y}\vec{z}} \cdot \) -
La contrainte équivalente permet de comparer l'état de contrainte multidimensionnel à un essai de traction par exemple.
Pour les poutres, on peut montrer que les contraintes équivalentes s'écrivent:
- Von Mises : \( \sqrt{\sigma^2+4\tau^2} \)
- Treca : \( \sqrt{\sigma^2+3\tau^2} \)
-
Toutes les parties d'une structure ne peuvent être assimilées à une poutre. Dans ce cas, les contraintes peuvent être déterminer par une méthode intégrée le plus souvent dans les modeleurs géométriques : la méthode des éléments finis. Elle est particulièrement intéressante quand il y a des concentrations de contraintes ou pour les pièce massives.
-
On veut dimensionner des tubes pour la structure suivante:
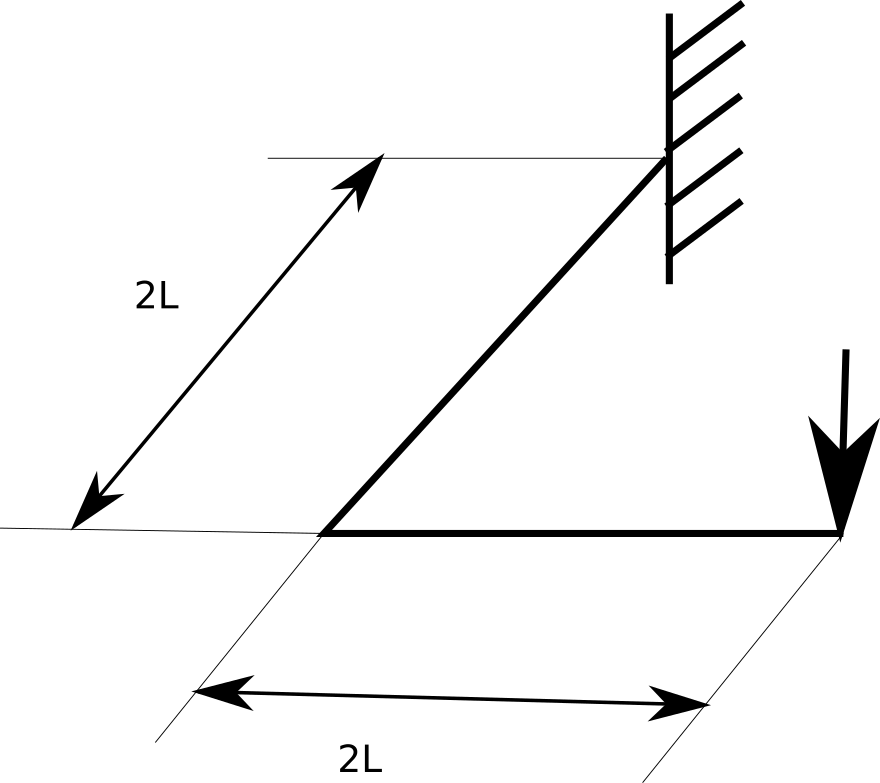
La longueur L est de 1m, la charge est de 500kg.
- Déterminer les actions de liaisons: \( X_A=0,Y_A=0,Z_A=F,L_A=F2L,M_A=-F2L,N_A=0 \)
- Déterminer alors le torseur de cohésion le long de la poutre.
- Calculer les contraintes au niveau d'un encastrement.
- Proposer une méthode pour trouver le diamètre et l'épaisseur des tubes.
- Déterminer les actions de liaisons: \( X_A=0,Y_A=0,Z_A=F,L_A=F2L,M_A=-F2L,N_A=0 \)