Flexion

Pour la flexion, le moment résultant induit par les contraintes : \( M_f = \int \sigma y dS \)

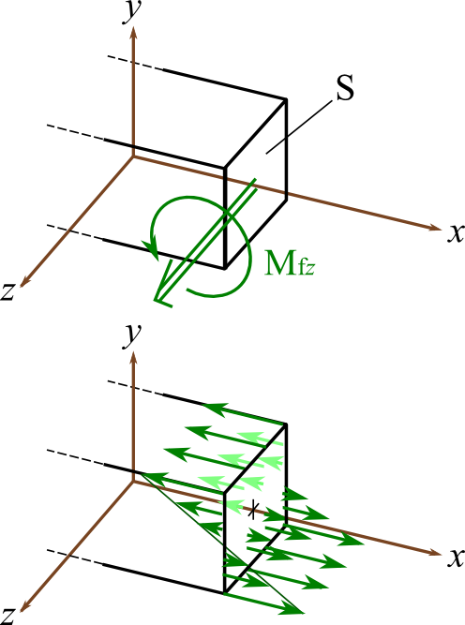
Après quelques calculs, on peut montrer que

\( \sigma = - \frac{M_{fz}}{I_{Gz}} y \)

On remarque que les contraintes ne sont plus homogènes dans la section et qu'elles dépendent de leur position par rapport au centre de la section (ligne neutre).

Le tenseur des contraintes s'écrit:\( \left [ \begin{matrix} \sigma(y)$& 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{matrix} \right ]_{\vec{x}\vec{y}\vec{z}} \)

Exemple

Une poutre rectangulaire de 100mm de haut et 50 mm  de large et 4mm d'épaisseur subit un moment fléchissant de 500000N.mm. Déterminer la contrainte en y=0 et y =50mm.

Calcul de I = \( \frac{100^3 50}{12}-\frac{92^3 42}{12}=1441258mm^4 \)

en y= 0, la contrainte est nulle

en y =50mm, la contrainte vaut \( -\frac{5000000}{1441258}50=-173MPa \)