Résumé de section

  • La contrainte est une action interne à la matière répartie sur la section. Elles équilibrent les actions extérieures. La résultante de ces actions réparties sont par définition égale au torseur de cohésion. Si on prend une facette dont la normale est celle de la section, les contraintes \( \sigma \) sont normales à la section. Par définition, la résultante de ces contraintes normales est l'effort normal du torseur de cohésion

    \( N = \int_S \sigma dS \)


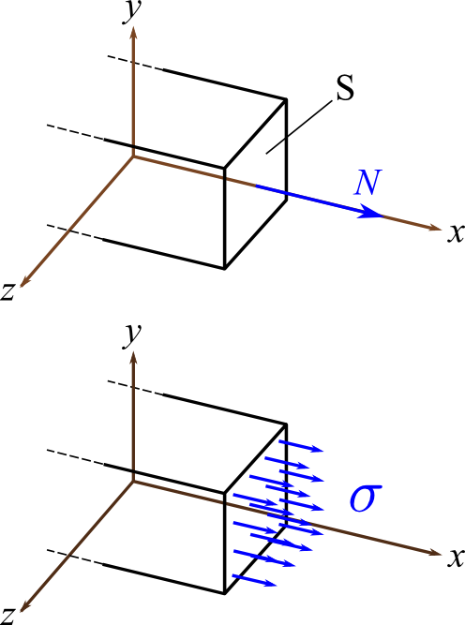
    Si la contrainte est constante dans toute la section, on a :

    \( N=\sigma S \) ou encore \( \sigma = \frac{N}{S} \)

    Le tenseur de contrainte s'écrit pour tout point de la section:

    \( \left [ \begin{matrix} \sigma & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0\end{matrix} \right ]_{\vec{x}\vec{y}\vec{z}} \)