Sollications composées
Résumé de section
-
En général, ces sollicitations sont composées entre elles:
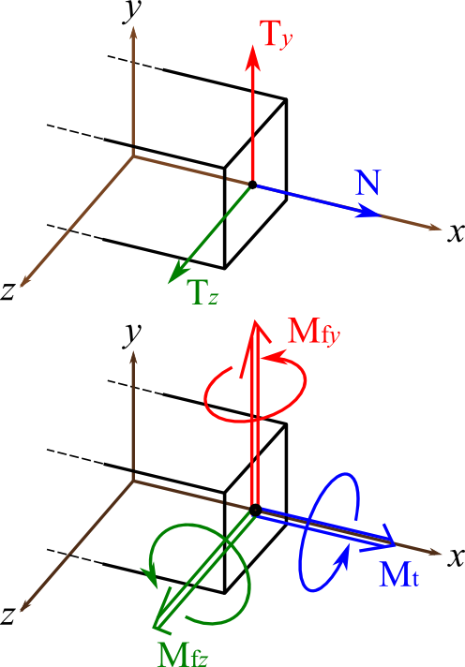
Dans ces conditions, les contraintes en un point s'additionnent.
Traction + Flexion sur z
Si on a le torseur de cohésion qui s'écrit:\( _G \left \{ \begin{tabular}{cc} N & $0$ \\ $0$ & $0$ \\ $0$ & $M_{f3}$\end{tabular} \right \}_{\vec{x}\vec{y}\vec{z}} \)L'effort normal crée des contraintes normales et uniformes dans la section:\( \left [ \begin{tabular}{ccc} $\sigma=\frac{N}{S}$ & 0 & 0 \\ 0 & $0$ & $0$ \\ $0$ & $0$ & $0$\end{tabular} \right ]_{\vec{x}\vec{y}\vec{z}} \cdot \)et la flexion autour de z (3) crée une contrainte qui varie dans la section:\( \left [ \begin{tabular}{ccc} $\sigma(y)=-\frac{M_{f3}}{I_{G3}} y$ & 0 & 0 \\ 0 & $0$ & $0$ \\ $0$ & $0$ & $0$\end{tabular} \right ]_{\vec{x}\vec{y}\vec{z}} \cdot \)au bout du compte, on a en tout point de la section:\( \left [ \begin{tabular}{ccc} $\frac{N}{S}-\frac{M_{f3}}{I_{G3}} y$ & 0 & 0 \\ 0 & $0$ & $0$ \\ $0$ & $0$ & $0$\end{tabular} \right ]_{\vec{x}\vec{y}\vec{z}} \cdot \)Torsion - Flexion d'un barreau cylindrique
Le torseur de cohésion s'écrit:\( _G \left \{ \begin{tabular}{cc} 0 & $M_t$ \\ $0$ & $0$ \\ $0$ & $M_{f3}$\end{tabular} \right \}_{\vec{x}\vec{y}\vec{z}} \)La flexion crée un état de contrainte:\( \left [ \begin{tabular}{ccc} $\sigma(y)=-\frac{M_{f3}}{I_{G3}} y$ & 0 & 0 \\ 0 & $0$ & $0$ \\ $0$ & $0$ & $0$\end{tabular} \right ]_{\vec{x}\vec{y}\vec{z}} \cdot \)et la torsion:\( \left [ \begin{tabular}{ccc} 0 & $\frac{M_t}{J}r$ & 0 \\ $\frac{M_t}{J}r$ & $0$ & $0$ \\ $0$ & $0$ & $0$\end{tabular} \right ]_{\vec{x}\vec{y}\vec{z}} \cdot \)Le tenseur des contraintes en un point s'écrit alors:\( \left [ \begin{tabular}{ccc} $-\frac{M_{f3}}{I_{G3}} y$ & $\frac{M_t}{J}r$ & 0 \\ $\frac{M_t}{J}r$ & $0$ & $0$ \\ $0$ & $0$ & $0$\end{tabular} \right ]_{\vec{x}\vec{y}\vec{z}} \cdot \)